Hi there!
引き続き、1冊読了したので書評(という名の個人的な感想)をメモっておきます。
今回読んだのがこちら、In Pursuit of the Unknown – 17 equations That Changed the Worlds です。

Summary
タイトルにもあるように、世の中のあり方をかえた17の代表的な方程式について、それぞれの歴史やどのように利用されているのかを説明してあります。
方程式ごとの章の初めに “What does it tell us?”:何を教えてくれるか?、”Why is that important?”:どのような点が重要なのか?、”What did it lead to?”:何を導いた(生み出した)か?についてまとめてあります。この辺り見るだけでも結構楽しかったりします。
例えば、ピタゴラスの定理 \(a^2+b^2=c^2\) については、
- 直角三角形の3つの辺の関係性についてを教えてくれて
- 座標における距離の測定や代数と幾何をリンクする点が重要であり
- 測量やナビ、もっと最近では特殊・一般相対性理論の基礎をなす
みたいなことが書いてあります。かの有名な相対性理論も元を辿ればピタゴラスの定理から出発しているって点が興味深いですね。
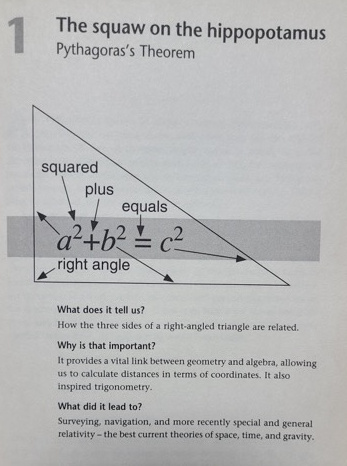
三角形の辺の長さ(頂点の距離)の関係性が、空間と時間と重力の関係性に発展していくって感じでしょうか。
上記みたいな感じで、色々な数式について述べてあります。個人的に面白かったのは、
- Pattern of chance – Normal Distribution
- Codes, communications, and computers – Information Theory
- The imbalance of nature – Chaos Theory
- The Midas formula – Black Scholes Equation
あたりですかね、もちろん全部興味深かったですが。
\( \displaystyle
\Phi(x)=\frac{1}{\sqrt{2\pi\sigma}}e^{ -\frac{(x-\mu)^2}{2\sigma^2}}
\)
Normal Distribution については、統計学、そして最近ではAIなんかの基礎になってる確率と統計の重要な概念なので、今後もっと深く調べてみたいなーと思いました。品質管理検定で統計的仮説検定や推定はある程度学んでいたので少し身近なテーマでした。
\( H = \ – \sum{ p(x) \log p(x)}\)
Information theory は、テクノロジー系のこと全般が好きなので、情報量の限界とかの話が面白かったですね。よく情報技術者試験でも出てくる誤り訂正ビットやハミング符合の話なんかもありました。
\( x_{t+1} = kx_{t}(1-x_{t})\)
Chaos Theory は、実はカオスとランダムは違う概念であって、ランダムは大体イメージ通りだけども、カオス(無秩序)は実は秩序の中から生まれるって話が良かったです。レーズンパンの生地をこねるシチュエーションで、任意の回数生地をこね回した時にレーズンが初期の位置からどのぐらい移動するかって説明は上手だなと思いました。
\( \displaystyle
\frac{1}{2}\sigma^{2} S^{2} \frac{\partial^{2} V}{\partial S^2}
+ r S \frac{\partial V}{\partial S}\
+ \frac{\partial V}{\partial t}
– r V
=0
\)
Black-Scholes Equationについては、あまりよく知りませんでしたが、これは実は金融派生商品いわゆるデリバティブやオプション、それから先物とかに関連する方程式ってことでした。リーマンショックがなぜ起きたのか?について、数式の観点から見ているとこが面白かったです。
相対性理論や波動方程式、シュレディンガー方程式については、難しすぎて何やらよくわかんなかったです、物理の勉強もっとせんといかんな、とは思いました。
後書(Where Next?)では、Theory of Everything (万物の理論)について、実はそんなものは存在しないのかも知れないって可能性も示唆されてました。
実は、世界は離散的で今まで考えられてきた連続的な数式から一旦離れなければならないかもしれない、って話も興味深いですね。一部のコンピュータサイエンスに造詣が深い科学者達はそのようにも考えてるみたいです。
Cellular Automata(セル・オートマトン)という離散的なモデルが、どのような点で従来の連続的な方程式に優っているのか、という話から、未来の数式は離散的なアルゴリズムのようなものに置き換わってるかもしれないって可能性に言及してました。
Opinion
読んでみて、やっぱり天才の発想と理論は半端じゃないなと思った反面、近現代のサイエンスの発達から見て、基本的な数式の理解は必要不可欠だなとも思いました。
数学ベースに興味のある物理の分野とかも学んでおかないと世の中に置いてかれるなーと。これだけ科学技術が発達して、科学技術に依存して生活が営まれている世においては特に。
とりあえず、代数 -> 確率と統計 -> AI関連 って感じで勉強進めようと思います。ということで引き続き、ALGEBRA – A complete introduction 読んでいきます。
However, it is still entirely credible that we might soon find new laws of nature based on discrete, digital structures and systems. The future may consist of algorithms, not equations. But until that day dawns, if ever, our greatest insights into nature’s laws take the form of equations, and we should learn to understand them and appreciate them. Equations have a track record. They really have changed the world – and they will change it again.
In Pursuit of the Unknown – 17 Equations That Changed the World by Ian Stewart. BASIC BOOKS: “Where Next?”



コメント